Półtora roku temu zadałem sobie po raz pierwszy pytanie „Czy można uruchomić program napisany w Haskellu na platformie .NET?” Sens takiego przedsięwzięcia jest taki, że programista .NET może korzystać w pewnym stopniu ze znanych mu bibliotek, jednocześnie korzystając z dobrodziejstw czystego programowania funkcyjnego. Ten post jest podstawą do poniższej prezentacji:
Leniwość i czystość
Zacznijmy od spojrzenia – jakie Haskell ma własności i dlaczego są pożądane. Haskell jest językiem funkcyjnym, czyli funkcje są na równi z innymi wartościami. Tak samo jak możemy manipulować liczbami, stosując na nich np. operację dodawania, tak samo możemy operować na funkcjach z operacją kompozycji.
Czystość (purity)
W matematyce wszystkie funkcje są czyste. Rozumiemy przez to brak „brudów” w postaci efektów ubocznych. Jeśli funkcja dostanie argument x, to niezależnie ile razy ją wywołamy, zawsze zwróci tę samą odpowiedź.
Czystość przekłada się na inną pożądaną własność – przezroczystość referencyjną (referential transparency). Dzięki niej jeśli używamy pewnego wyrażenia kilka razy, to możemy obliczyć je tylko raz i wszędzie przekazywać wynik.
f a <~> f a <~> fa === let x = f a in x <~> x <~> x
Note: zastosowanie tej własności nie wpływa na wynik, ale może wpłynąć na sposób jego obliczenia, np. wykonując mniej pracy albo wykonując pracę z innym użyciem pamięci.
Leniwość
Kiedy wszystkie funkcje są czyste, kolejność wykonywania niezależnych działań staje się mniej istotna. Dzięki temu możemy opóźnić wykonanie obliczeń aż do momentu, kiedy będą nam one faktycznie potrzebne. Być może okaże się, że możemy się bez nich obyć.
Spójrzmy na przykład: mamy w ręku listę liczb liczby. Chcemy znaleźć pierwszą liczbę na tej liście, której kwadrat jest większy od 100. Możemy użyć leniwych operacji, które będą wykonywane w miarę potrzeby i napisać
szukana = pierwsza (> 100) $ map kwadrat liczby
Gdzie: funkcja kwadrat podnosi liczbę do kwadratu; funkcja map przyjmuje modyfikator listy, listę i zwraca nową listę gdzie do każdego elementu zaaplikowano modyfikator; operator $ aplikuje lewą stronę do prawej (analogicznie jak <|) żeby ominąć nawiasy; funkcja pierwsza przyjmuje warunek i listę, a następnie zwraca pierwszy element listy spełniający ten warunek, lub kończy się błędem.
Gdyby map działało gorliwie i podnosiło wszystkie elementy listy liczby do kwadratu, to mogłoby wykonać dużo niepotrzebnej pracy, jeśli już pierwszy element spełnia warunek. Dlatego lista, którą zwraca map jest leniwa. Będziemy na bieżąco, w trakcie sprawdzania warunku, obliczali kolejne wartości.
Ktoś może zapytać, dlaczego nie napisać odrębnej funkcji, która połączyłaby funkcjonalność map i pierwsza i jednocześnie wykonywała operację i sprawdzała warunek, wykonując tylko tyle pracy ile trzeba. Otóż siłą programowania jest kompozycja mniejszych prostszych funkcji. W programowaniu funkcyjnym staramy się pisać uniwersalne, abstrakcyjne funkcje, które następnie połączone razem tworzą coś nowego, bardziej wyspecjalizowanego. Wprowadzając do języka leniwość, abstrahujemy nad kolejnością wykonywania działań przez komputer.
Co więcej, przez to że leniwość jest wpisana w język, nie odróżniamy obliczonej już listy od nieobliczonej. Możemy jednorodnie działać na leniwych i gorliwych typach danych. W przykładzie mieliśmy konkretną listę liczb, ale w praktyce ona również może być leniwa. Co więcej, jej elementy mogą być dynamicznie czytane z dysku, lub pobierane przez internet. Ale funkcja, która przetwarza tę listę, jest czysta i nie interesuje jej skąd te dane się biorą.
Zapamiętywanie wyników obliczeń
Żeby leniwość działała, nie tylko odkładamy obliczenia na później, ale także spamiętujemy wyniki. Dzięki temu przeprowadzając dwa działania na tej samej leniwej liście elementów, obliczymy ich wartości tylko raz.
let l = map fib [1..10]
in (map (+1) l, map (*2) l)
To wyrażenie zwraca dwie leniwe listy, jedna to pierwsze 10 liczb Fibonacciego powiększone o 1, a druga to te same 10 liczb, ale pomnożone razy 2. Kiedy poprosimy o 5-ty element pierwszej listy, aby go wypisać, zostanie obliczone wyrażenie fib 5 + 1. Ale l zostanie zaktualizowane, więc kiedy będziemy chcieli wypisać 5-ty element drugiej listy to dostaniemy do obliczenia wyrażenie 8 * 2, bo obliczyliśmy już wcześniej, że l[5] wynosi 8 (fib 5).
Obliczanie leniwych wyrażeń
O programie funkcyjnym można myśleć jak o grafie wyrażeń. Przy pomocy mechanizmów redukcji tego grafu będziemy obliczali kolejne wartości. W historii było kilka różnych podejść do efektywnej kompilacji leniwych języków programowania do kodu maszynowego. Na ten moment najpowszechniej używaną, zaimplementowaną w kompilatorze Haskella GHC, techniką jest Spineless Tagless G-Machine, która operuje na rozszerzonym rachunku lambda.
Poza standardową aplikacją i abstrakcją funkcji w rachunku lambda, mamy dwie operacje let..in oraz case..of, a także ograniczenie, że funkcje mogą być tylko aplikowane do atomów: stałych prymitywnych danych lub zmiennych związanych przy pomocy konstrukcji let.
Kiedy maszyna napotyka w programie wyrażenie let x = expr1 in expr2 to tworzy nowy obiekt w pamięci odpowiadający obliczeniu expr1 i posługuje się wskaźnikiem na ten obiekt wykonując dalej obliczenie expr2. Taki obiekt nazwiemy „thunk”. Jeśli kiedyś będziemy potrzebowali wartości jaką niesie thunk, to wykonamy kod, na który wskazuje, a następnie zmodyfikujemy jego strukturę tak, aby przy kolejnych prośbach o wartość, od razu zwracał to co już raz wyliczył.
Kiedy możemy chcieć wymusić obliczenie jakiegoś wyrażenia? Wtedy kiedy potrzebujemy sprawdzić jego wartość. Będą to wyrażenia takiej postaci:
case c_expr of
con1 -> expr1
con2 -> expr2
DEFAULT -> expr3
Gdzie sprawdzamy, czy wartość sprawdzanego wyrażenia pasuje do którejś alternatywy, a następnie wykonujemy odpowiadający jej kawałek kodu. W szczególności wyrażenie warunkowe if..then..else zostanie zapisane jako
case condition of
True -> thenExpr
False -> elseExpr
Mając aplikację funkcji, abstrakcję (wyrażanie lambda), przypisania let i wyliczenia case można wyrazić wszystkie programy. W praktyce język STG ma jeszcze odrębne konstrukcje do aplikowania operatorów i konstruktorów danych.
GHC kompiluje kod Haskella do kodu maszynowego lub do LLVM (na potrzeby np. platformy ARM), stosując przy tym masę optymalizacji i wyciskając z maszyny naprawdę dobrą wydajność. Myśląc o przeniesieniu tego kodu na platformę z narzuconymi ograniczeniami, taką jak .NET, trzeba się liczyć ze spadkiem tej niesamowitej wydajności. Zyskujemy wtedy głównie na leniwej semantyce oraz czytelności kodu, który piszemy.
Haskell na .NET
Mierząc się z problemem kompilacji Haskella na .NET, zacząłem od próby stworzenia środowiska uruchomieniowego, które stanowi podstawę abstrakcyjnych konceptów i obiektów, na których będzie bazować kod użytkownika.
Poniższe rozwiązanie jest efektem wielu podejść do problemu, a po jego opisaniu opowiem trochę o tych wcześniejszych podejściach.
Zacznę od wprowadzenia jednostki obliczenia Closure. Za każdym razem kiedy napotkamy let będziemy chcieli przypisać do zmiennej referencję do obliczenia. Może to być obliczenie stałe, które zawsze zwraca określoną wartość. Natomiast kiedy będziemy potrzebowali sprawdzić naszą obliczoną wartość w wyrażeniu case, to sięgniemy po metodę Eval() na obiekcie Closure.
Dane
W dalszej części będziemy się posługiwać 3 konstruktorami danych:
Int : I(int)
List : Nil()
: Cons(Closure, Closure)
Konstruktory danych dziedziczą po klasie Data, która dziedziczy po klasie Closure. Obiekt z danymi to niejako obliczenie zwracające jedną wartość – ten sam obiekt. To jest przykład tej wspomnianej nierozróżnialności między danymi obliczonymi i leniwymi.
Zauważmy, że konstruktory dziedziczą bezpośrednio po typie Data, a nie np. po typie List. Otóż w Haskellu typy są bardziej złożonym konceptem niż w .NET-cie i postanowiłem skorzystać z idei „type erasure”, skupiając się tym samym bardziej na reprezentacji danych w pamięci. Kod w Haskellu nie będzie korzystał z refleksji, więc nie będzie kodu potrzebującego informacji o typach. Może to być natomiast uciążliwe z punktu widzenia użytkownika kodu, który musi wiedzieć na jakich typach operuje dany konstruktor.
Kolejna rzecz jaką zyskujemy przez usunięcie typów to uproszczona struktura typów związanych z zapamiętywaniem obliczeń. Kiedy Cons dostaje obiekt typu Closure to nie interesuje go, czy jest to już wyliczone wyrażenie, czy nie. W tej sytuacji jesteśmy w stanie podać tam obiekt typu Thunk, który nie musi nic wiedzieć o typie danych, które będzie obliczał. Natomiast gdyby Cons przyjmował Int i List<Int>, to odłożone obliczenia musiałyby być ich podklasami. Co powodowałoby zwiększenie ilości generowanych typów.
Kiedy sprawdzamy konstruktory możemy sie posłużyć albo ich typami, albo ich tagiem. W praktyce dla wyrażeń case z małą liczbą (<5) alternatyw bardziej opłaca się sprawdzać konstruktory po typie.
public sealed class Cons : Data
{
public Closure x0;
public Closure x1;
public override int Tag => 1;
public Cons(Closure x0, Closure x1)
{
this.x0 = x0;
this.x1 = x1;
}
}
Note: w całym runtimie pola z danymi są publiczne i nazwane x0 do xN aby ułatwić ich manipulację.
Praktyczny przykład
Poniżej znajduje się przykład skompilowanej funkcji map (uproszczony):
// Haskell
// map _ [] = []
// map f (x:xs) = f x : map f xs
// STG
// map = \r [] [f, l] ->
// case l of
// [] -> []
// h : t -> let nh = \u [f,h] [] -> f h
// nt = \u [f,t] [] -> map f t
// in (nh : nt)
public static Closure map_Entry(Closure f, Closure l)
{
l = l.Eval();
switch (l)
{
default:
throw new ImpossibleException();
case Nil l_Nil:
return new Nil();
case Cons l_Cons:
var h = l_Cons.x0;
var t = l_Cons.x1;
var nt = Updatable.Make(map_Entry, f, t);
var nh = Updatable.Make(StgApply.Apply, f, h);
return new Cons(nh, nt);
}
}
Chcemy sprawdzić któremu konstruktorowi odpowiada lista l. Jeśli l jest leniwym thunkiem, to musimy przeprowadzić odpowiednie obliczenia – dlatego wywołujemy l.Eval(). Następnie sprawdzamy typ wyniku i jeśli jest to lista pusta, to zwracamy nową listę pustą, a jeśli głowa i ogon, to tworzymy dwa thunki, które reprezentują obliczenie nowej głowy i nowego ogona i zwracamy nowy obiekt Cons. Tutaj Updatable.Make przyjmuje funkcję do wywołania oraz jej argumenty.
Thunki
W przykładzie powyżej zobaczyliśmy funkcję Updatable.Make, który tworzy nowy thunk – odłożone obliczenie. W jaki sposób thunki działają?
Podstawą będzie abstrakcyjna klasa Thunk:
public abstract class Thunk : Closure
{
public Closure ind;
protected abstract Closure Compute();
protected internal virtual void Cleanup() { }
public override Closure Eval()
{
if (ind != null) return ind.Eval();
ind = Blackhole.Instance; // detect loop
ind = Compute();
Cleanup();
return ind;
}
}
Nasz thunk ma wskaźnik na obliczone dane (ind od indirection), i jeśli nie jest to null to kiedy poprosimy o obliczenie wartości thunka metodą Eval() zostanie nam zwrócony.
Natomiast jeśli jeszcze nie wykonaliśmy obliczenia, to tymczasowo ustawiamy naszą wartość na czarną dziurę i wywołujemy metodę Compute(), aby obliczyć wartość. Gdyby się okazało, że do obliczenia wartości potrzebujemy tej wartości, to w celu wczesnego zatrzymania programu nasza czarna dziura rzuci wyjątek. Jak dostaniemy wynik obliczenia, to przypisujemy go pola ind i wykonujemy czyszczenie, a potem zwracamy wartość.
Czyszczenie ma na celu zwolnienie referencji do danych, które potrzebne nam były do obliczenia wartości, ale po jej obliczeniu mogą zostać odśmiecone przez Garbage Collector (GC).
Użytkownik będzie używał klas z rodziny Updatable, dziedziczących po Thunk, które przyjmują wskaźnik do metody zawierającej kod obliczenia oraz wolne zmienne, przekazywane jako argumenty tej metody.
public unsafe class Updatable<T0> : Thunk
{
protected internal void* f;
public T0 x0;
public Updatable(void* f, T0 x0)
{
this.f = f;
this.x0 = x0;
}
protected override Closure Compute()
=> CLR.TailCallIndirectGeneric<T0, Closure>(x0, f);
protected internal override void Cleanup()
=> x0 = default;
}
Funkcje
Podstawą funkcji będzie klasa Function:
public abstract class Function : Closure
{
public override Closure Eval() => this;
public override ClosureType Type => ClosureType.Function;
public abstract int Arity { get; }
public abstract R Apply<A0, R>(A0 a0);
public abstract R Apply<A0, A1, R>(A0 a0, A1 a1);
public abstract R Apply<A0, A1, A2, R>(A0 a0, A1 a1, A2 a2);
}
Tak samo jak dane, obliczając funkcję po prostu ją zwracamy - Eval() => this.
Każda funkcja zna swoją arność (Arity), która jest używana podczas aplikacji.
Na ten moment mój runtime jest kompatybilny z funkcjami o maksymalnie 3 argumentach. W praktyce, dzięki własności „currying”, funkcja np. 4-argumentowa po otrzymaniu 3 argumentów może zwrócić nową funkcję jedno-argumentową.
Podobnie jak w przypadku thunków, użytkownik będzie korzystał z rodziny klas Fun, dziedziczących po Function.
public unsafe class Fun<F0> : Fun
{
public F0 x0;
public Fun(int arity, void* f, F0 x0) : base(arity, f)
=> this.x0 = x0;
public override R Apply<A0, R>(A0 a0)
=> CLR.TailCallIndirectGeneric<F0, A0, R>(x0, a0, f);
public override R Apply<A0, A1, R>(A0 a0, A1 a1)
=> CLR.TailCallIndirectGeneric<F0, A0, A1, R>(x0, a0, a1, f);
public override R Apply<A0, A1, A2, R>(A0 a0, A1 a1, A2 a2)
=> CLR.TailCallIndirectGeneric<F0, A0, A1, A2, R>(x0, a0, a1, a2, f);
}
Klasy Fun implementują wszystkie warianty metod Apply, natomiast w zależności od arności tylko jedna z nich na danym obiekcie będzie wołana. Te metody są generyczne dla ułatwienia, to wołający wie jakie typy przekazuje i czego oczekuje. Bugi w kompilatorze Haskella do C# mogą więc powodować błędy już po uruchomieniu.
W przypadku gdybyśmy chcieli mieć jedną klasę per arność (z jedną metodą apply) i per wolne zmienne, to tych klas byłoby kilkukrotnie więcej. Nie ma przesłanek wydajnościowych ku takiemu rozwiązaniu, więc z punktu widzenia utrzymania kodu runtime’u powyższe rozwiązanie jest lepsze.
Aplikacja funkcji
Istnieją dwa modele aplikacji funkcji na STGM: Eval/Apply i Push/Enter. Zdecydowałem się na ten pierwszy, ponieważ jest bardziej „natywny” dla platformy .NET. W przypadku Push/Enter mielibyśmy do czynienia z utrzymywaniem kilku stosów argumentów co jest mniej efektywne niż przekazywanie argumentów w rejestrach.
Zatem do aplikacji funkcji posłużą nam pomocnicze statyczne metody w klasie StgApply
public static R Apply<A0, A1, R>(Closure func, A0 a0, A1 a1)
{
switch (func.Type)
{
case ClosureType.Function:
return ApplyFun<A0, A1, R>(func as Function, a0, a1);
case ClosureType.PartialApplication:
return (func as PAP).Apply<A0, A1, R>(a0, a1);
case ClosureType.Data:
throw new Exception($"Cannot apply a value ({func.GetType()})");
default:
func = func.Eval();
return Apply<A0, A1, R>(func, a0, a1);
}
}
private static R ApplyFun<A0, A1, R>(Function f, A0 a0, A1 a1)
{
switch (f.Arity)
{
case 1:
var h = f.Apply<A0, Closure>(a0);
return Apply<A1, R>(h, a1);
case 2:
return f.Apply<A0, A1, R>(a0, a1);
default:
return (R)(object)new PAP<A0, A1>(f, a0, a1);
}
}
Note: ten kod jest nieobiektowy i zgodnie ze sztuką cała ta logika byłaby umieszczona w metodach tychże typów.
Obiekty częściowej aplikacji to instancje rodziny klas PAP, które przechowują argumenty i kiedy dostają więcej argumentów to ponownie wołają metody pomocnicze z StgApply.
public sealed class PAP<B0> : PAP
{
public B0 x0;
public PAP(Function f, B0 x0) : base(f)
=> this.x0 = x0;
public override R Apply<A0, R>(A0 a0)
=> StgApply.Apply<B0, A0, R>(f, x0, a0);
public override R Apply<A0, A1, R>(A0 a0, A1 a1)
=> StgApply.Apply<B0, A0, A1, R>(f, x0, a0, a1);
}
CLR intrinsics
Mieliście okazję zobaczyć wskaźniki do funkcji o typie void* oraz magiczne funkcje
CLR.TailCallIndirectGeneric<...>(..., f);
Jest to hack, aby zmodyfikowany kompilator C# emitował instrukcje CIL calli. Analogicznie, wszędzie tam gdzie chcemy uzyskać wskaźnik musimy posłużyć się
CLR.LoadFunctionPointer(fun);
żeby kompilator wyemitował instrukcję ldftn. Wszędzie tam gdzie tworzymy instację Fun lub Updatable to będziemy w ten sposób pobierać wskaźnik.
Dlaczego używam tychże wskaźników, a nie delegatów funkcji, czyli “bezpiecznych” wskaźników na funkcje? Ze względu na prędkość ich tworzenia.
Poprzednie koncepty
Teraz przejdziemy przez kilka konceptów które pojawiały się wcześniej podczas mojej pracy nad tym runtimem.
Stos, ogonowość i kontynuacje
Na platformie .NET stos jest ograniczony. Przy każdym wywołaniu funkcji odkładamy na stos wskaźnik powrotu. Przy dużej ilości wywołań funkcji możemy dojść do sytuacji kiedy skończy nam się miejsce na stosie.
W przypadku funkcji rekurencyjnych rozwiązaniem jest rekurencja ogonowa, gdy wyrażeniem, które zwracamy jest wynik wywołania funkcji. Wtedy zamiast odkładać wskaźnik powrotu, po prostu skaczemy do kolejnej funkcji. Wiele funkcji można przekształcić do formy ogonowej, dzięki czemu stają się tak szybkie jak pętle.
Ale czasami będziemy potrzebować zachować na stosie jakieś dane, których użyjemy po powrocie z wołanej funkcji do dalszych obliczeń. Byłem przekonany, że ograniczony stos będzie dla mnie klęską i od początku próbowałem starać się minimalizować jego wielkość.
W tym celu używałem kontynuacji alokowanych na stercie. Inicjalizujemy kontynuację z danymi, które będą nam później potrzebne i wskaźnikiem na funkcję, którą należy będzie wywołać, a następnie skaczemy do funkcji, którą teraz chcemy obliczyć. Ta funkcja musi być świadoma istnienia kontynuacji i zwrócić do niej swój wynik.
Spójrzmy na zmodyfikowany przykład map z powyżej:
public static Closure map_Entry(StgContext ctx, Closure f, Closure l)
{
return ctx.Eval(l, StgCont.Make(map_Case_l, f));
}
public static Closure map_Case_l(StgContext ctx, Closure l, Closure f)
{
switch (l)
{
default:
throw new ImpossibleException();
case Nil l_Nil:
return ctx.Return(new Nil());
case Cons l_Cons:
var h = l_Cons.x0;
var t = l_Cons.x1;
var nt = Updatable.Make(map_Entry, f, t);
var nh = Updatable.Make(StgApply.Apply, f, h);
return ctx.Return(new Cons(nh, nt));
}
}
Kontynuacja ma prosty interfejs
public abstract class Continuation
{
public abstract Closure Call(StgContext ctx, Closure c);
/** The next continuation in the stack. */
protected internal Continuation next;
public Continuation With(Continuation cont)
{
next = cont;
return this;
}
}
Po zakończeniu ewaluacji odbędzie się Call do kontynuacji. Kontynuacje tworzą stos na bazie linked-listy, co jest używane w metodach Push,Pop i Return kontekstu.
Jednak koszt alokacji, a później odśmiecania, powoduje, że ta technika jest mniej wydajna niż operowanie na stosie operacyjnym. Odpowiednie zarządzanie ogonowością i gorliwością w Haskellu będzie prowadziło do lepszych programów i zmniejszy zapotrzebowanie na stos.
Ponadto, ponieważ kontynuacje nie były generycznym rozwiązaniem, to nie było możliwości ich zastosowania dla typów prymitywnych, które nadal operowały na stosie.
Zmniejszanie ilości alokacji
W celu zmniejszenia ilości alokacji ramek Update do aktualizacji thunków i ramek Id do zwracania wyników, zaimplementowałem proste pule obiektów zwiększane w miarę zapotrzebowania.
sealed class UpdatePool {
private List<Update> pool;
private int index;
public UpdatePool(int initSize) {
pool = new List<Update>(initSize);
for (int i = 0; i < initSize; i++)
pool.Add(new Update());
index = 0;
}
public Update Get(Thunk t) {
if (index < pool.Count) {
var u = pool[index++];
u.t = t;
return u;
} else {
var u = new Update();
pool.Add(u);
index++;
u.t = t;
return u;
}
}
public void Return(Update u) {
u.t = null; //free thunk to GC
index--;
}
}
To przełożyło się szczególnie na wzrost wydajności kiedy nie dochodziło do odśmiecania podczas pracy na bardzo wysokim stosie operacyjnym. Żeby GC wiedział co ma odśmiecać, przechodzi po stosie w poszukiwaniu wskaźników, a gdy ten stos jest wielki to zajmuje mu to więcej czasu.
Kontynuacje w pętli
Zanim kontynuacje były ustawione w łańcuch i ogonowo wołane jedna po drugiej, to kontekst zawierał wyłącznie stos, a do aplikowania kolejnych kontynuacji służyła pętla:
static class StgEval
{
public static Closure EvalThen(StgContext ctx, Closure c, Continuation cont)
{
ctx.Push(cont);
return c.Eval(ctx); // continue the trampoline from continuation
}
public static Closure Eval(StgContext ctx, Closure next)
{
next = next.Eval(ctx);
if (!ctx.Empty)
{
Continuation cont = ctx.Pop();
next = cont.Call(ctx, next);
return Eval(ctx, next);
}
return next;
}
}
Takie rozwiązanie miałoby lepsze zastosowanie w przypadku braku wywołań ogonowych w postaci skoków, gdzie wysokość stosu rośnie znacznie szybciej.
Kompilacja Haskella do C#
Żeby móc testować mój runtime i porównywać do kodu produkowanego przez GHC postanowiłem napisać program w Haskellu korzystający z biblioteki GHC do otrzymania struktury STG, przed jej transformacją do C–. Kompilator jest niedokończony, między innymi dlatego, że sporo elementów GHC nie jest ładnie opisanych i trzeba przeczesywać kod źródłowy w poszukiwaniu odpowiedzi.
Natomiast główna część dotycząca kompilacji wyrażeń działa. Poniżej prezentuję mapping wyrażeń STG na C#:
- literały są przepisywane
- aplikacja funkcji
-
jeśli nie ma argumentów, to jest to zwrot wartości zmiennej
x --> x.Eval() -
jeśli ma argumenty, aplikujemy
f a --> StgApply.Apply<A,R>(f, a) -
jeśli ma argumenty i jest znaną funkcją
f a --> f__Entry(a)
-
-
aplikacja konstruktorów
Con a b --> new Con(a, b) - aplikacja operatorów – w zależności od operatora
-
w szczególności operatory logiczne konwertowane są na liczby
(x <= 0) ? 1 : 0
-
-
ewaluacja i wybór alternatywy
case x of DEFAULT -> ... alt1 -> ... alt2 -> ...-
jeśli zmienna jest unlifted to po prostu robimy switch
switch (x) { case 1: ... case 2: ... default: ... } -
jeśli zmienna jest lifted to najpierw ją zewalujemy a potem rozpakujemy
var le = l.Eval(); switch (le) { case Nil le_Nil: ... case Cons le_Cons: var h = le_Cons.x0; var t = le_Cons.x1; ... default: throw new ImpossibleException(); }
-
- przypisanie
- przypadek przypisań rekurencyjnych sprowadza się do tego, że najpierw tworzymy obiekty podstawiając
nulltam gdzie wskazujemy na inny obiekt, a potem przypisujemy je z powrotem -
przypisanie danych jest normalne
let x = Con a b --> var x = new Con(a, b) -
przypisanie closure polega na wygenerowaniu metody z obliczeniem i stworzeniu nowego obiektu
let f = \r [] [x] -> x + 1 --> var f = new Fun(1, CLR.LoadFunctionPointer(f__Entry)); ... public static long f__Entry(long x) { return x + 1; }
- przypadek przypisań rekurencyjnych sprowadza się do tego, że najpierw tworzymy obiekty podstawiając
Nazwy lokalnych zmiennych są zmieniane na unikatowe, żeby nie było problemów, że dwie metody nazywają się tak samo.
Performance
Spotkałem się z wieloma zagadnieniami dotyczącymi optymalności pisanego przeze mnie kodu i udało mi się określić kilka wąskich gardeł.
Branching
Kiedy jeszcze pracowałem z kontynuacjami na stercie, zadałem sobie pytanie czy nie byłoby szybciej jeśli ominę krok ewaluacji i wejścia w kontynuację gdy dane już są zewaluowane? Warunki są kosztowne jeśli branch predictor się pomyli. W moich testach wyszło, że pominięcie warunku daje lepsze rezultaty.
Alokacje
Tworzenie dużej liczby obiektów na stercie prowadzi do częstszego odśmiecania, które zajmuje sporo czasu.
Otwarte i zamknięte klasy
Zamknięte klasy (sealed) mają parę plusów. Jeśli odwołujemy się do metody na zmknietej klasie, to kompilator może posłużyć się procesem dewirtualizacji i wołać odpowiednią metodę statycznie z pominięciem tablicy metod. W przypadku konstruktorów danych zamknięcie pozwala na przeprowadzanie sprawdzenia typu przez porównanie wskaźnika na tablicę metod z określoną wartością, zamiast przechodzenia po drzewie dziedziczenia.
Odpowiednie struktury danych
Chociażby to, że łańcuch kontynuacji był szybszy niż stos kontynuacji.
Mój runtime (Lazer) vs GHC
Poniżej prezentuję tabelę porównującą czasy wykonania prostych algorytmów. W ogólności mój runtime działa w zakresie 1x-2.5x tyle co GHC, co jest bardzo dobrym wynikiem.
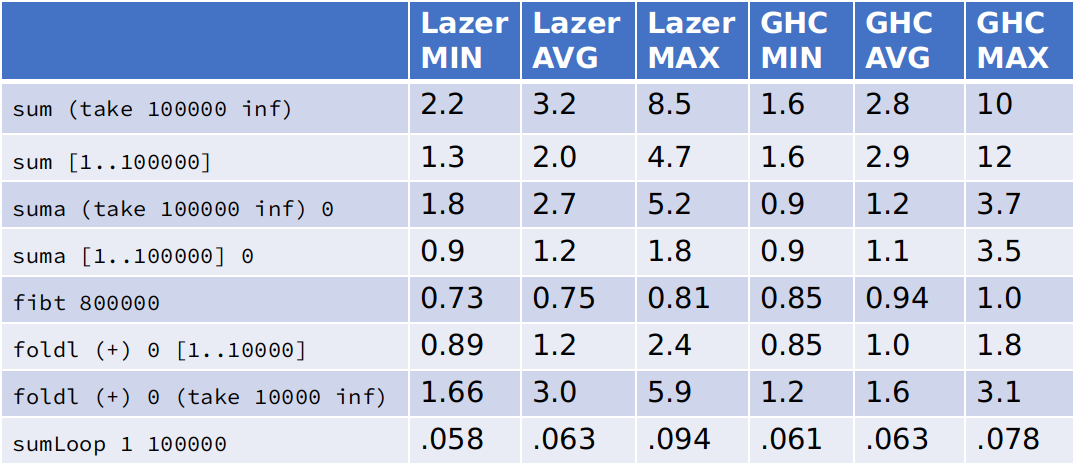
Kod testów w Haskellu:
sum :: [Int] -> Int
sum [] = 0
sum (x:xs) = x + sum xs
suma :: [Int] -> Int -> Int
suma [] !a = a
suma (x:xs) !a = suma xs (x+a)
take :: Int -> [a] -> [a]
take 0 = \_ -> []
take n = \l -> case l of
[] -> []
(h:t) -> h : take (n-1) t
inf = 1 : (map (+1)) inf
fiba :: Int -> Int -> Int -> Int
fiba !a !b n = if n <= 0 then a else
let next = a + b in fiba b next (n-1)
fibt = fiba 0 1
foldl f x0 xs = foldl_go x0 xs
where
foldl_go x0 [] = x0
foldl_go x0 (x:xs) =
let app = (f x0 x) in
foldl_go app xs
sumLoop :: Int -> Int -> Int
sumLoop from to = go from to 0
where go !f !t !n | f > t = n
| otherwise = go (f+1) t (n+f)Podsumowanie
Kod do mojej pracy znajdziesz na GitHubie manio143/Lazer.